Timelike Showers

1. Main variables
2. Effective coupling constants
3. Lower cutoffs
4. QED Radiation in particle decays
5. Interleaved evolution
6. Global recoil
7. Weak showers
8. Further radiation modification options
9. Options for non-singular and higher-order terms
10. Switch off branching types

The normal user is not expected to call TimeShower directly, but only have it called from Pythia. Nonetheless, some of the parameters below, in particular TimeShower:alphaSvalue, would be of interest for uncertainty estimates and tuning exercises. Note that PYTHIA also incorporates an automated framework for shower uncertainty variations.

Main variables

mode  TimeShower:pTmaxMatch   (default = 1; minimum = 0; maximum = 2)
Way in which the maximum shower evolution scale is set to match the scale of the hard process itself.
option 0 : (i) if the final state of the hard process (not counting subsequent resonance decays) contains at least one quark (u, d, s, c ,b), gluon or photon then pT_max is chosen to be the factorization scale for internal processes and the scale value for Les Houches input; (ii) if not, emissions are allowed to go all the way up to the kinematical limit (i.e. to half the dipole mass). This option agrees with the corresponding one for spacelike showers. There the reasoning is that in the former set of processes the ISR emission of yet another quark, gluon or photon could lead to double-counting, while no such danger exists in the latter case. The argument is less compelling for timelike showers, but could be a reasonable starting point.
option 1 : always use the factorization scale for an internal process and the scale value for Les Houches input, i.e. the lower value. This should avoid double-counting, but may leave out some emissions that ought to have been simulated. (Also known as wimpy showers.)
option 2 : always allow emissions up to the kinematical limit (i.e. to half the dipole mass). This will simulate all possible event topologies, but may lead to double-counting. (Also known as power showers.)
Note 1: as enumerated in the text, these options take effect both for internal and external processes. Whether a particular option makes sense depends on the context. For instance, if events for the same basic process to different orders are to be matched, then option 1 would be a reasonable first guess. But in more sophisticated descriptions option 2 could be combined with UserHooks vetoes on emissions that would lead to double-counting, using more flexible phase space boundaries. Further details are found in the Matching and Merging description, with an example in examples/main152. Option 0, finally, may be most realistic when only Born-level processes are involved, possibly in combination with a nonzero TimeShower:pTdampMatch.
Note 2: These options only apply to the hard interaction. If a "second hard" process is present, the two are analyzed and set separately for the default 0 option, while both are affected the same way for non-default options 1 and 2. Emissions off subsequent multiparton interactions are always constrained to be below the factorization scale of each process itself. The options also assume that you use interleaved evolution, so that FSR is in direct competition with ISR for the hardest emission. If you already generated a number of ISR partons at low pT, it would not make sense to have a later FSR shower up to the kinematical limit for all of them.
Note 3: Recall that resonance decays are not affected by this mode, but that showers there are always set to fill the full phase space, often with built-in matrix-element-matching that give a NLO accuracy. A modification of this behaviour would require you to work with UserHooks. However, for Les Houches input the optional Beams:strictLHEFscale = on setting restricts all emissions, also in resonance decays, to be below the input scale value.

parm  TimeShower:pTmaxFudge   (default = 1.0; minimum = 0.25; maximum = 2.0)
In cases where the above pTmaxMatch rules would imply that pT_max = pT_factorization, pTmaxFudge introduces a multiplicative factor f such that instead pT_max = f * pT_factorization. Only applies to the hardest interaction in an event, and a "second hard" if there is such a one, cf. below. It is strongly suggested that f = 1, but variations around this default can be useful to test this assumption.
Note:Scales for resonance decays are not affected, but can be set separately by user hooks.

parm  TimeShower:pTmaxFudgeMPI   (default = 1.0; minimum = 0.25; maximum = 2.0)
A multiplicative factor f such that pT_max = f * pT_factorization, as above, but here for the non-hardest interactions (when multiparton interactions are allowed).

mode  TimeShower:pTdampMatch   (default = 0; minimum = 0; maximum = 4)
These options only take effect when a process is allowed to radiate up to the kinematical limit by the above pTmaxMatch choice, and no matrix-element corrections are available. Then, in many processes, the fall-off in pT will be too slow by one factor of pT^2. That is, while showers have an approximate dpT^2/pT^2 shape, often it should become more like dpT^2/pT^4 at pT values above the scale of the hard process. This argument is more obvious and relevant for ISR, where emissions could go the the kinematical limit, whereas they are constrained by the respective dipole mass for FSR. Nevertheless this matching option is offered for FSR to have a (semi-)symmetric description. Note that a dampening factor is applied to all dipoles in the final state of the hard process, which is somewhat different from the ISR implementation.
option 0 : emissions go up to the kinematical limit, with no special dampening.
option 1 : emissions go up to the kinematical limit, but dampened by a factor k^2 Q^2_fac/(pT^2 + k^2 Q^2_fac), where Q_fac is the factorization scale and k is a multiplicative fudge factor stored in pTdampFudge below.
option 2 : emissions go up to the kinematical limit, but dampened by a factor k^2 Q^2_ren/(pT^2 + k^2 Q^2_ren), where Q_ren is the renormalization scale and k is a multiplicative fudge factor stored in pTdampFudge below.
option 3 : as option 1, but in addition to the standard requirements for dampening it is further necessary to have at least two top or beyond-the-Standard-Model coloured particles in the final state. Examples include t tbar and squark gluino production.
option 4 : as option 2, but in addition to the standard requirements for dampening it is further necessary to have at least two top or beyond-the-Standard-Model coloured particles in the final state. Examples include t tbar and squark gluino production.
Note: These options only apply to the hard interaction. Specifically, a "second hard" interaction would not be affected. Emissions off subsequent multiparton interactions are always constrained to be below the factorization scale of the process itself.

parm  TimeShower:pTdampFudge   (default = 1.0; minimum = 0.25; maximum = 4.0)
In cases 1 and 2 above, where a dampening is imposed at around the factorization or renormalization scale, respectively, this allows the pT scale of dampening of radiation by a half to be shifted by this factor relative to the default Q_fac or Q_ren. This number ought to be in the neighbourhood of unity, but variations away from this value could do better in some processes.

Effective coupling constants

The amount of QCD radiation in the shower is determined by

parm  TimeShower:alphaSvalue   (default = 0.1365; minimum = 0.06; maximum = 0.25)
The alpha_strong value at scale M_Z^2. The default value corresponds to a crude tuning to LEP data, to be improved.

The actual value is then regulated by the running to the scale pT^2, at which the shower evaluates alpha_strong.

mode  TimeShower:alphaSorder   (default = 1; minimum = 0; maximum = 3)
Order at which alpha_strong runs,
option 0 : zeroth order, i.e. alpha_strong is kept fixed.
option 1 : first order, which is the normal value.
option 2 : second order. Since other parts of the code do not go to second order there is no strong reason to use this option, but there is also nothing wrong with it.
option 3 : third order, with the same comment as for second order. The expression in the 2006 RPP is used here.

The CMW rescaling of Lambda_QCD (see the section on StandardModelParameters) can be applied to the alpha_strong values used for timelike showers. Note that tunes using this option need lower values of alpha_strong(m_Z^2) than tunes that do not.

flag  TimeShower:alphaSuseCMW   (default = off)

option off : Do not apply the CMW rescaling.
option on : Apply the CMW rescaling, increasing Lambda_QCD for timelike showers by a factor roughly 1.6.

The following options for taming (regularising) the effective value of the strong coupling at low (IR) scales are available:

parm  TimeShower:alphaSmax   (default = -1.; minimum = -1.; maximum = 10.)
For alphaSmax > 0, the effective value of the strong coupling in timelike shower branchings is capped at this value, effectively freezing it in the infrared. Any value alphaSmax ≤ 0 is interpreted to mean that no such constraint should be imposed.

parm  TimeShower:alphaSrenormShift   (default = 0.; minimum = 0.; maximum = 4.)
The position of the Landau pole for timelike shower branchings is shifted by evaluating the strong coupling at scale2 → scale2 + x * Lambda_QCD(nF=3)^2, with x = renormShift. The default value of x=0 corresponds to no shift. A value of x=1 corresponds to shifting the pole to an input scale of zero. For larger values, the effective coupling at zero input scale is finite and equal to 4 pi / (9 ln(x)). Since the scale argument is typically only shifted by a few hundred MeV, changes to the value of the effective coupling at perturbative input scales (well above Lambda_QCD(nF=3)) are generally small. The main effect is thus a suppression of the value of the effective coupling near the shower pTmin cutoff. For uncertainty estimates, variations of this parameter by a factor 2-4 in either direction (for a given central choice) may be a reasonable starting point. Detailed examinations of this assumption would be welcome.

QED radiation is regulated by the alpha_electromagnetic value at the pT^2 scale of a branching.

mode  TimeShower:alphaEMorder   (default = 1; minimum = -1; maximum = 1)
The running of alpha_em.
option 1 : first-order running, constrained to agree with StandardModel:alphaEMmZ at the Z^0 mass.
option 0 : zeroth order, i.e. alpha_em is kept fixed at its value at vanishing momentum transfer.
option -1 : zeroth order, i.e. alpha_em is kept fixed, but at StandardModel:alphaEMmZ, i.e. its value at the Z^0 mass.

The natural scale for couplings, and PDFs for dipoles stretching out to the beam remnants, is pT^2. To explore uncertainties it is possibly to vary around this value, however, in analogy with what can be done for hard processes. (Note that there is also an automated framework for shower uncertainties.)

parm  TimeShower:renormMultFac   (default = 1.; minimum = 0.1; maximum = 10.)
The default pT^2 renormalization scale is multiplied by this prefactor. For QCD this is equivalent to a change of Lambda^2 in the opposite direction, i.e. to a change of alpha_strong(M_Z^2) (except that flavour thresholds remain at fixed scales).

parm  TimeShower:factorMultFac   (default = 1.; minimum = 0.1; maximum = 10.)
The default pT^2 factorization scale is multiplied by this prefactor.

Lower cutoffs

The rate of radiation if divergent in the pT → 0 limit. Here, however, perturbation theory is expected to break down. Therefore an effective pT_min cutoff parameter is introduced, below which no emissions are allowed. The cutoff may be different for QCD and QED radiation off quarks, and is mainly a technical parameter for QED radiation off leptons.

parm  TimeShower:pTmin   (default = 0.5; minimum = 0.1; maximum = 2.0)
Parton shower cut-off pT for QCD emissions.

parm  TimeShower:pTminChgQ   (default = 0.5; minimum = 0.1; maximum = 2.0)
Parton shower cut-off pT for photon coupling to coloured particle.

parm  TimeShower:pTminChgL   (default = 1e-6; minimum = 1e-10; maximum = 2.0)
Parton shower cut-off pT for pure QED branchings. Assumed smaller than (or equal to) pTminChgQ.

Shower branchings gamma → f fbar, where f is a quark or lepton, in part compete with the hard processes involving gamma^*/Z^0 production. In order to avoid overlap it makes sense to correlate the maximum gamma mass allowed in showers with the minimum gamma^*/Z^0 mass allowed in hard processes. In addition, the shower contribution only contains the pure gamma^* contribution, i.e. not the Z^0 part, so the mass spectrum above 50 GeV or so would not be well described.

parm  TimeShower:mMaxGamma   (default = 10.0; minimum = 0.001; maximum = 5000.0)
Maximum invariant mass allowed for the created fermion pair in a gamma → f fbar branching in the shower.

QED Radiation in particle decays

Note:This option only takes effect if HadronLevel:QED = on.

Traditionally, PYTHIA did not have a generic machinery for handling QED radiation in hadron (and tau) decays. In order to include this, a program like PHOTOS [Bar94, Dav10] could be used as an afterburner. The options below can be used to enable PYTHIA's internal shower machinery for QED radiation.
Note 1: Only two-body decays can be handled.
Note 2: The f → fγ DGLAP kernels are used indiscriminately irrespective of actual spins.
Note 3: First-order matrix-element corrections for the first (hardest) photon emission are applied to V0 → ll and V± → l nu since such decays are mediated by gamma^*/Z^0/ W^+- exchange, for which PYTHIA does have an existing machinery that can be applied.

mode  TimeShower:gammaModeHad   (default = 1; minimum = 1; maximum = 2)
When HadronLevel:QED = on and the simple-shower model is used, this switch determines how to handle hadron-level photon radiation.
option 1 : Photon radiation only in two-body decays to a lepton pair, see above. Matrix element corrections are only applied in the case of V0 → ll and V± → l nu, based on the equivalent corrections for Z and W decays.
option 2 : Photon radiation in all two-body hadron decays. Note: this option is mainly intended for comparisons and not for serious studies. Since the simple shower's splitting kernels do not encode the correct Lorentz structures for hadron decays in many cases, nor are the correct matrix-element corrections implemented, this option is not expected to deliver a faithful description of QED radiation in hadron decays. (Nor are hadronic form factors or photon VMD effects taken into account.)

Interleaved evolution

There is no corresponding requirement for final-state radiation (FSR) to be interleaved. Such an FSR emission does not compete directly for beam energy (but see below), and also can be viewed as occurring after the other two components in some kind of time sense. Interleaving is allowed, however, since it can be argued that a high-pT FSR occurs on shorter time scales than a low-pT MPI, say. Backwards evolution of ISR is also an example that physical time is not the only possible ordering principle, but that one can work with conditional probabilities: given the partonic picture at a specific pT resolution scale, what possibilities are open for a modified picture at a slightly lower pT scale, either by MPI, ISR or FSR? Complete interleaving of the three components also offers advantages if one aims at matching to higher-order matrix elements above some given scale.

flag  TimeShower:interleave   (default = on)
If on, final-state emissions are interleaved in the same decreasing-pT chain as multiparton interactions and initial-state emissions. If off, final-state emissions are only addressed after the multiparton interactions and initial-state radiation have been considered.

Whether such interleaving affects resonance decays or not is controlled by the following switch:

flag  TimeShower:interleaveResDec   (default = off)
When this flag is set to off, the interleaved evolution does not affect showering in resonance decays, such as a Z^0. These decays are only introduced after the production process has been considered in full, and the subsequent FSR is carried out inside the resonance, with preserved resonance mass. When this flag is set to on, resonance decays are inserted in the final-state shower evolution when it reaches the pT scale defined by TimeShower:resDecScaleChoice below.

When TimeShower:interleaveResDec is set to on, the pT scale at which interleaved resonance decays are inserted in the shower evolution is determined by the value of the following switch:

mode  TimeShower:resDecScaleChoice   (default = 1; minimum = 0; maximum = 2)

option 0 : The on-shell width of the resonance.
option 1 : Off-shellness determined by |m² - m0²|/m0. This implies, e.g., that the decay of a resonance which has m = m0 ± Γ will be performed at a scale pT ~ sqrt(2) Γ.
option 2 : Off-shellness determined by sqrt(|m² - m0²|). This implies, e.g., that the decay of a resonance which has m = m0 ± Γ will be performed at a scale pT ~ sqrt(2 Γ m0 ).

Technically, the following steps happen when an interleaved resonance decay is inserted in the evolution:

• The resonance is replaced by its decay products;
• A final-state resonance shower is performed within the resonance-decay system (with preserved resonance mass) bringing it down to the same pT scale that the rest of the evolution had reached before the decay was inserted.
• The overall final-state shower evolution is continued from that pT scale downwards, now with the resonance replaced by its decay products together with any branchings that happened during the resonance shower in the previous step.

Note that, since interleaving of resonance decays only affects the shower evolution below the scale at which the resonance decays occur, only mild effects are expected for SM resonances like t, Z, and W, which all have widths not much larger than 1 GeV. The dynamic scale choices, especially TimeShower:resDecScaleChoice = 2, however, allow for potentially larger effects in the tails.

One aspect of FSR for a hard process in hadron collisions is that often colour dipoles are formed between a scattered parton and a beam remnant, or rather the hole left behind by an incoming partons. If such holes are allowed as dipole ends and take the recoil when the scattered parton undergoes a branching then this translates into the need to take some amount of remnant energy also in the case of FSR, i.e. the roles of ISR and FSR are not completely decoupled. The energy taken away is bookkept by increasing the x value assigned to the incoming scattering parton, and a reweighting factor x_new f(x_new, pT^2) / x_old f(x_old, pT^2) in the emission probability ensures that not unphysically large x_new values are reached. Usually such x changes are small, and they can be viewed as a higher-order effect beyond the accuracy of the leading-log initial-state showers.

This choice is not unique, however. As an alternative, if nothing else useful for cross-checks, one could imagine that the FSR is completely decoupled from the ISR and beam remnants.

flag  TimeShower:allowBeamRecoil   (default = on)
If on, the final-state shower is allowed to borrow energy from the beam remnants as described above, thereby changing the mass of the scattering subsystem. If off, the partons in the scattering subsystem are constrained to borrow energy from each other, such that the total four-momentum of the system is preserved. This flag has no effect on resonance decays, where the shower always preserves the resonance mass, cf. the comment above about showers for resonances never being interleaved.

flag  TimeShower:dampenBeamRecoil   (default = on)
When beam recoil is allowed there is still some ambiguity how far into the beam end of the dipole that emission should be allowed. It is dampened in the beam region, but probably not enough. When on an additional suppression factor 4 pT2_hard / (4 pT2_hard + m2) is multiplied on to the emission probability. Here pT_hard is the transverse momentum of the radiating parton and m the off-shell mass it acquires by the branching, m2 = pT2/(z(1-z)). Note that m2 = 4 pT2_hard is the kinematical limit for a scattering at 90 degrees without beam recoil.

When there is no interleaving, a number of MPIs may have been generated before FSR is considered. In principle there could be colour correlations between the MPIs, such that a final-state colour of one MPI could be matched by the corresponding final-state anticolour of another MPI. These thereby would form a colour dipole, but one that does not come out from a common vertex, and therefore presumably could not radiate in full. Currently the standard procedure is to match colours between MPIs only after FSR, so MPI systems would radiate independently, with recoils taken by the beam remnant, where necessary. This could change, however, and the following switch would then regulate the choice of behaviour.

flag  TimeShower:allowMPIdipole   (default = off)
If on, and if interleaving is off, then dipoles are allowed to be formed between matching final-state colour-anticolour pairs also between two different MPIs. Else dipoles can normally only form inside the same MPI, and the could-have-been dipoles between different MPIs instead appear as dipoles stretched to the beam remnants. In either case a dipole can still form between two MPIs if a final-state colour cannot be matched inside the same MPI. This should normally not happen, except if rescattering is allowed, whereby two or more MPIs get interconnected.

Global recoil

Technically, the radiation pattern is most conveniently represented in the rest frame of the final state of the hard subprocess. Then, for each parton at a time, the rest of the final state can be viewed as a single effective parton. This "parton" has a fixed invariant mass during the emission process, and takes the recoil without any changed direction of motion. The momenta of the individual new recoilers are then obtained by a simple common boost of the original ones.

This alternative approach will miss out on the colour coherence phenomena. Specifically, with the whole subcollision mass as "dipole" mass, the phase space for subsequent emissions is larger than for the normal dipole algorithm. The phase space difference grows as more and more gluons are created, and thus leads to a way too steep multiplication of soft gluons. Therefore the main application is for the first one or few emissions of the shower, where a potential overestimate of the emission rate is to be corrected for anyway, by matching to the relevant matrix elements. Thereafter, subsequent emissions should be handled as before, i.e. with dipoles spanned between nearby partons. Furthermore, only the first (hardest) subcollision is handled with global recoils, since subsequent MPI's would not be subject to matrix element corrections anyway.

In order for the mid-shower switch from global to local recoils to work, colours are traced and bookkept just as for normal showers; it is only that this information is not used in those steps where a global recoil is requested. (Thus, e.g., a gluon is still bookkept as one colour and one anticolour dipole end, with half the charge each, but with global recoil those two ends radiate identically.)

flag  TimeShower:globalRecoil   (default = off)
Alternative approach as above, where all final-state particles share the recoil of an emission.
If off, then use the standard dipole-recoil approach.
If on, use the alternative global recoil, but only for the first interaction, and only while the number of particles in the final state is at most TimeShower:nMaxGlobalRecoil before the branching.

mode  TimeShower:nMaxGlobalRecoil   (default = 2; minimum = 1)
Represents the maximum number of particles in the final state for which the next final-state emission can be performed with the global recoil strategy. This number counts all particles, whether they are allowed to radiate or not, e.g. also Z^0. Also partons created by initial-state radiation emissions counts towards this sum, as part of the interleaved evolution. Without interleaved evolution this option would not make sense, since then a varying and large number of partons could already have been created by the initial-state radiation before the first final-state one, and then there is not likely to be any matrix elements available for matching.

Two variations of the scheme outlined above are also available, (motivated by comparative studies within aMC@NLO). These studies indicate that global recoils should be used as sparsely as possible, in order to retain desirable features of the radiation pattern produced with the local recoil prescription.

mode  TimeShower:globalRecoilMode   (default = 0; minimum = 0; maximum = 2)
Choice which splittings are produced with the global recoil approach.
option 0 : Global recoil mode as outlined above, i.e. using global recoils until the number of final state particles exceeds TimeShower:nMaxGlobalRecoil.
option 1 : Global recoil only for the first branching of final state legs that have an ancestor in the hard process, and if the maximal number of branchings generated according to the global recoil scheme (see TimeShower:nMaxGlobalBranch below) has not yet been reached.
option 2 : Global recoil only if the first branching in the whole evolution is a timelike splitting of a parton in an event with Born-like kinematics (i.e.\ an S-event). The impact of global recoils should be minimal in this case. This option is only sensible for interleaved evolution.

mode  TimeShower:nMaxGlobalBranch   (default = -1)
The maximum number of splittings in the final state for which the next final-state emission can be performed with the global recoil strategy. This number has to be set if TimeShower:globalRecoilMode = 1 or TimeShower:globalRecoilMode = 2

mode  TimeShower:nPartonsInBorn   (default = -1)
The number of partons for Born-like phase space points. This number needs to be set if a different treatment of S-events (with Born-like kinematics) and H-events (with real-emission kinematics) is desired. This number has to be set if TimeShower:globalRecoilMode = 2.

flag  TimeShower:limitPTmaxGlobal   (default = off)
If on, limit the maximal pT produced in branchings in the global recoil scheme exactly as in the default (local) scheme. This means that the mass of the splitting dipole will set an upper bound for the pT of an emission. To be more explicit, this disallows emissions with pT larger than min{μ_start ², m_D²/4}, with m_D² = (√ (p_r +p_s)² -m_0,s)² - m_0,r² , where the shower starting scale is μ_start (i.e. SCALUP when reading LHE files, and Info.QFac() otherwise), r the radiating parton, and s the recoiling particle that would have been used in the local recoil scheme. This option is only used if wimpy showers are enabled.

The global-recoil machinery does not work well with rescattering in the MPI machinery, since then the recoiling system is not uniquely defined. MultipartonInteractions:allowRescatter = off by default, so this is not a main issue. If both options are switched on, rescattering will only be allowed to kick in after the global recoil has ceased to be active, i.e. once the nMaxGlobalRecoil limit has been exceeded. This should not be a major conflict, since rescattering is mainly of interest at later stages of the downwards pT evolution.

Further, it is strongly recommended to set TimeShower:MEcorrections = off (not default!), i.e. not to correct the emission probability to the internal matrix elements. The internal ME options do not cover any cases relevant for a multibody recoiler anyway, so no guarantees are given what prescription would come to be used. Instead, without ME corrections, a process-independent emission rate is obtained, and user hooks can provide the desired process-specific rejection factors.

Weak showers

flag  TimeShower:weakShower   (default = off)
Allow a weak shower, yes or no.

mode  TimeShower:weakShowerMode   (default = 0; minimum = 0; maximum = 2)
Determine which branchings are allowed.
option 0 : both W^+- and Z^0 branchings.
option 1 : only W^+- branchings.
option 2 : only Z^0 branchings.

parm  TimeShower:pTminWeak   (default = 1.0; minimum = 0.1; maximum = 2.0)
Parton shower cut-off pT for weak branchings.

Further radiation modification options

Matrix-element corrections

flag  TimeShower:MEcorrections   (default = on)
Use of matrix element corrections where available; on/off = true/false.

flag  TimeShower:MEextended   (default = on)
Use matrix element corrections also for 1 → n and 2 → n processes where no matrix elements are encoded, by an attempt to match on to one of the 1 → 2 processes that are implemented. This should at least provide relevant mass dampening for massive radiators and recoilers. Only has a meaning if MEcorrections above is switched on.

flag  TimeShower:MEafterFirst   (default = on)
Use of matrix element corrections also after the first emission, for dipole ends of the same system that did not yet radiate. Only has a meaning if MEcorrections above is switched on. Switching off this option currently does not take effect for a few rare types of secondary branchings, where ME corrections play a central role.

flag  TimeShower:skipFirstMECinHardProc   (default = off)
Allow control of matrix element corrections (MECs) in the hard process. By default, a matching is made between the final state of a hard process and the suite of decay MECs. When this option is "on", no MEC is used until after the first emission. This allows compatability with various NLO-correct merging schemes.

mvec  TimeShower:skipFirstMECinResDecIDs   (default = {})
Allow control of matrix element corrections (MECs) in resonance decays, similarly to the treatment of the hard process. See above explanation. Only those resonance with the listed PDG identifiers are affected.

Weights for gluon (and photon) splittings

mode  TimeShower:weightGluonToQuark   (default = 4; minimum = 1; maximum = 8)
Different options to assign kinematics distributions and weights for g → q qbar branchings, notably for charm and bottom quarks. These options also have the corresponding effect on gamma → f fbar branchings. The rationale for the options is described in this note.
Notation: r_q = m_q^2/m_qq^2, beta = sqrt(1 - 4r_q), with m_q the quark mass and m_qq the q qbar pair invariant mass. The scale factor k is described below, TimeShower:scaleGluonToQuark.
option 1 : same splitting kernel (1/2) (z^2 + (1-z)^2) for massive as massless quarks, only with an extra beta phase space factor.
option 2 : a splitting kernel (beta/2) (z^2 + (1-z)^2 + 8r_q z(1-z)).
option 3 : a splitting kernel z^2 + (1-z)^2 + 8r_q z(1-z), normalized so that the z-integrated rate is (beta/3) (1 + r/2).
option 4 : same as 3, but additionally a suppression factor (1 - m_qq^2/m_dipole^2)^3, which reduces the rate of high-mass q qbar pairs.
option 5 : same as 1, but reweighted to an alpha_s(k m_qq^2) rather than the normal alpha_s(pT^2).
option 6 : same as 2, but reweighted to an alpha_s(k m_qq^2) rather than the normal alpha_s(pT^2).
option 7 : same as 3, but reweighted to an alpha_s(k m_qq^2) rather than the normal alpha_s(pT^2).
option 8 : same as 4, but reweighted to an alpha_s(k m_qq^2) rather than the normal alpha_s(pT^2).

parm  TimeShower:scaleGluonToQuark   (default = 1.0; minimum = 0.25; maximum = 1.0)
Extra scale parameter k for TimeShower:weightGluonToQuark options 5 - 8. Comes on top of TimeShower:renormMultFac, which affects alpha_s(pT^2) alike.

Gluon polarization effects

flag  TimeShower:phiPolAsym   (default = on)
Azimuthal asymmetry induced by gluon polarization; on/off = true/false.

flag  TimeShower:phiPolAsymHard   (default = on)
Extend the above azimuthal asymmetry (if on) also back to gluons produced in the hard process itself, where feasible; on/off = true/false.

Dead cone effect

flag  TimeShower:recoilDeadCone   (default = on)
For topologies where a gluon recoils against a massive quark (or another massive coloured particle) there are no suitable ME corrections implemented into PYTHIA. When the dipole radiation pattern is split into two ends, with a smooth transition between the two, this means that the gluon end can radiate into the quark hemisphere as if the quark were massless. The "dead cone" effect, that radiation collinear with a massive quark is strongly suppressed, thereby is not fully respected. (Unlike radiation from the quark end itself, where mass effects are included.) With this switch on, a further suppression is therefore introduced for g → g g branchings, derived as the massive/massless ratio of the eikonal expression for dipole radiation, which kills radiation collinear with the quark. The g → q qbar branchings currently are not affected; the absence of a soft singularity implies that there is hardly any radiation into the recoiler hemisphere anyway.

Resonance-final dipoles

mode  TimeShower:recoilStrategyRF   (default = 0; minimum = 0; maximum = 1)
In the decays of coloured resonances, notably t → b W, it is not possible to set up dipoles with matched colours inside the final state. In the first emission the b radiator therefore has W as recoiler, and that choice is unique. A matrix-element correction is also applied for this branching. Once a gluon has been radiated, however, there are two dipoles to consider. One colour line connects the gluon to the b, and the other to the t. The first line is a traditional dipole, so no problem, but the second resonance-final (RF) one needs attention. Also in subsequent shower steps there will always be one RF colour line. This switch allows two different alternative strategies to be applied for radiation off the final-state end of such a dipole.
option 0 : Let the W act as recoiler when the parton with the top colour radiates. Before version 8.160 this was the only possibility, which could give too much wide-angle radiation. From version 8.314 onwards, the parameter TimeShower:weightRF allows to suppress this wide-angle radiation by a factor proportional to the RF eikonal, which should deliver a better description of RF radiation patterns.
option 1 : Assign the b as recoiler for both colour lines of the first emitted gluon, i.e. also the one with the top colour. This assignment then is inherited in the subsequent shower evolution. This option was the default between versions 8.160 and 8.313.
Note 1: Up to and including version 8.309 options 0 and 1 were available as the off/on options of the TimeShower:recoilToColoured flag.
Note 2: The same issue exists for QED radiation, but obviously is less significant. Consider the example W → e nu, where originally the nu takes the recoil. In option 0 the nu would remain recoiler, while in option 1 instead each newly emitted photon becomes the new recoiler.

For TimeShower:recoilStrategyRF = 0, the following parameter and flag allow to apply a correction to the emission pattern for RF dipoles. The intention is that the radiation pattern should attach to the one expected for a final-initial dipole, while the recoil of this radiation is taken by the final particle that best correlates with the original top momentum.

parm  TimeShower:weightRF   (default = 1.; minimum = 0.; maximum = 1.)
In RF dipoles such as that which carries the colour of the top quark in t → b W, for TimeShower:recoilStrategyRF = 0 the W is chosen as recoiler not only for the first emission but also for subsequent emissions. The emission probability is corrected by a factor 1. + weightRF (eikTop/eikW - 1.), where eikTop is an eikonal factor in which the top is considered to be the recoiler while eikW is an eikonal factor in which the W is considered to be the recoiler. Thus, for weightRF = 0 the radiation pattern is uncorrected (and then corresponds to that for the W as recoiler), while for weightRF = 1 it is corrected by a factor eikTop/eikW. As a technical note, the denominator eikonal factor depends on the TimeShower:recoilDeadCone flag. If on, the radiation pattern has already been corrected for the W mass effects. Therefore the denominator eikonal will also contain the W mass term. If off, the denominator will not contain this term, such that the ratio introduces the mass correction. For TimeShower:recoilStrategyRF = 0, this parameter allows to smoothly interpolate between applying the full RF eikonal reweighting factor (obtained with the default value of weightRF = 1.) and no reweighting (for weightRF = 0.).

flag  TimeShower:recoilRFUseParents   (default = off)
The weightRF factor above is normally evaluated with the four-momenta of the three partons that have been produced by the dipole emission. If this flag is set to on, instead the radiator and recoiler momenta before the emission are used. The radiated parton obviously only exists afterwards, so there the choice is unique. The eikonal is valid in the soft-emission limit, where the two choices agree, but the off option better attaches to the singularity structure of matrix elements also for harder emissions. The on still represents a valid variation.
Note: weightRF and recoilRFuseParents have no effect for TimeShower:recoilStrategyRF = 1.

Factorization scale and PDFs

flag  TimeShower:useFixedFacScale   (default = off)
Allow the possibility to use a fixed factorization scale, set by the parm below. This option is unphysical and only intended for toy-model and debug studies.

parm  TimeShower:fixedFacScale   (default = 100.; minimum = 1.)
The fixed factorization scale, in GeV, that would be used in the evaluation of parton densities if the flag above is on.

mode  TimeShower:pdfMode   (default = 0; minimum = 0; maximum = 2)
This setting should not be touched by non-experts. Deviating from the default setting will only lead to consistent results after explicit external intervention. This setting can be useful in the context of interfaces to external code as done when using the flag Merging:runtimeAMCATNLOInterface described under Merging.
option 0 : this default setting corresponds to the typical shower treatment of including PDF ratios for dipole recoils in the initial state, leading to the generation of normal no-emission probabilities.
option 1 : disable the PDF dependence, which leads to the generation of Sudakov factors according to the momentum sum rule.
option 2 : disable the PDF dependence, which leads to the generation of Sudakov factors like option 1, but with a lower cut-off zMin = 0.5 on the energy-fraction integral.

Options for non-singular and higher-order terms

The parameters below are intended to explore uncertainties/variations arising from process-dependent non-singular terms and/or undetermined higher-order corrections to the effective branching kernels, beyond LL accuracy. This uses generalized forms of the shower splitting kernels, for gluon emissions and splittings respectively,

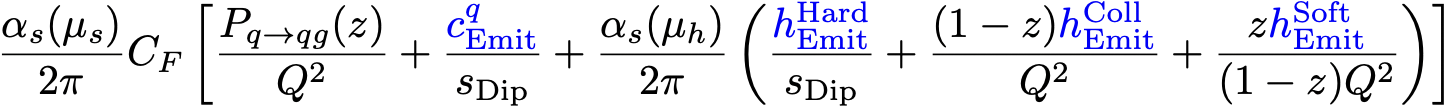
where μ_s is the standard renormalisation scale used for shower branchings and we take the scale for the second-order correction terms to be μ_h = mDip/4. The form used for the g→gg kernel is completely analogous to the one for q→qg above, with its own c coefficient but the same h coefficients.

First-order non-singular terms

For processes that do not have matrix-element corrections (MECs), the parameters below allow to add a constant (non-singular) term to the effective LO kernels for QCD branchings. For positive (negative) values, this increases (decreases) the branching probabilities. These terms are analogous to the ones called cNS in the context of uncertainty variations, and have the effect of modifying the splitting kernels as P(z)/Q2 → P(z)/Q2 + c.

parm  TimeShower:cEmitQ   (default = 0.0; minimum = -5.0; maximum = 5.0)
Non-singular term, c, for Q→QG branchings.

parm  TimeShower:cEmitC   (default = 0.0; minimum = -5.0; maximum = 5.0)
Additional non-singular term for C→CG branchings so that the total for such branchings is cEmitQ + cEmitC.

parm  TimeShower:cEmitB   (default = 0.0; minimum = -5.0; maximum = 5.0)
Additional non-singular term for B→BG branchings so that the total for such branchings is cEmitQ + cEmitB.

parm  TimeShower:cEmitG   (default = 0.0; minimum = -5.0; maximum = 5.0)
Non-singular term, c, for G→GG branchings.

parm  TimeShower:cSplit   (default = 0.0; minimum = -5.0; maximum = 5.0)
Non-singular term, c, for G→QQbar splittings.

parm  TimeShower:cSplitC   (default = 0.0; minimum = -5.0; maximum = 5.0)
Additional non-singular term for G→CCbar splittings so that the total for such splittings is cSplit + cSplitC.

parm  TimeShower:cSplitB   (default = 0.0; minimum = -5.0; maximum = 5.0)
Additional non-singular term for G→BBbar splittings so that the total for such splittings is cSplit + cSplitB.

Higher-order terms

The following parameters allow to add terms that are suppressed by an additional power of the strong coupling, representing variations of the effective branching kernels beyond LO and hence active also in the presence of MECs.

parm  TimeShower:hEmitHard   (default = 0.0; minimum = -40.0; maximum = 40.0)
Non-singular 2nd-order term added to Q→QG and G→GG branchings. Acts in the same way as the LO c parameters above but is suppressed by an extra power of α_S/(2π).

parm  TimeShower:hEmitColl   (default = 0.0; minimum = -20.0; maximum = 20.0)
Collinear-singular 2nd-order term added to Q→QG and G→GG branchings, proportional to (α_S/(2π))² z*P(z)/Q².

parm  TimeShower:hEmitSoft   (default = 0.0; minimum = -20.0; maximum = 20.0)
Soft-singular 2nd-order term added to Q→QG and G→GG branchings, proportional to (α_S/(2π))² (1-z)*P(z)/Q². Note that, when using the CMW scheme for the strong coupling, this parameter should not be allowed to differ significantly from zero (though small values could still be used to explore effective 3rd-order variations).

parm  TimeShower:hSplitHard   (default = 0.0; minimum = -40.0; maximum = 40.0)
Non-singular 2nd-order term added to G→QQ branchings. Acts in the same way as the LO c parameters above but is suppressed by an extra power of α_S/(2π).

parm  TimeShower:hSplitColl   (default = 0.0; minimum = -20.0; maximum = 20.0)
Collinear-singular 2nd-order term added to G→QQ branchings, proportional to (α_S/(2π))² P(z)/Q².

Switch off branching types

flag  TimeShower:QCDshower   (default = on)
Allow a QCD shower, i.e. branchings q → q g, g → g g and g → q qbar; on/off = true/false.

mode  TimeShower:nGluonToQuark   (default = 5; minimum = 0; maximum = 5)
Number of allowed quark flavours in g → q qbar branchings (phase space permitting). A change to 4 would exclude g → b bbar, etc.

flag  TimeShower:QEDshowerByQ   (default = on)
Allow quarks to radiate photons, i.e. branchings q → q gamma; on/off = true/false.

flag  TimeShower:QEDshowerByL   (default = on)
Allow leptons to radiate photons, i.e. branchings l → l gamma; on/off = true/false.

flag  TimeShower:QEDshowerByOther   (default = on)
Allow charged resonances to radiate photons, i.e. branchings q∼ → q∼ gamma; on/off = true/false. This will also allow the W boson to radiate.

flag  TimeShower:QEDshowerByGamma   (default = on)
Allow photons to branch into lepton or quark pairs, i.e. branchings gamma → l+ l- and gamma → q qbar; on/off = true/false.

mode  TimeShower:nGammaToQuark   (default = 5; minimum = 0; maximum = 5)
Number of allowed quark flavours in gamma → q qbar branchings (phase space permitting). A change to 4 would exclude gamma → b bbar, etc.

mode  TimeShower:nGammaToLepton   (default = 3; minimum = 0; maximum = 3)
Number of allowed lepton flavours in gamma → l+ l- branchings (phase space permitting). A change to 2 would exclude gamma → tau+ tau-, and a change to 1 also gamma → mu+ mu-.

flag  TimeShower:recoilToColoured   (default = on)
In the decays of coloured resonances, say t → b W, it is not possible to set up dipoles with matched colours. Originally the b radiator therefore has W as recoiler, and that choice is unique. Once a gluon has been radiated, however, it is possible either to have the unmatched colour (inherited by the gluon) still recoiling against the W (off), or else let it recoil against the b also for this dipole (on). Before version 8.160 the former was the only possibility, which could give unphysical radiation patterns. It is kept as an option to check backwards compatibility. The same issue exists for QED radiation, but obviously is less significant. Consider the example W → e nu, where originally the nu takes the recoil. In the old (off) scheme the nu would remain recoiler, while in the new (on) instead each newly emitted photon becomes the new recoiler.